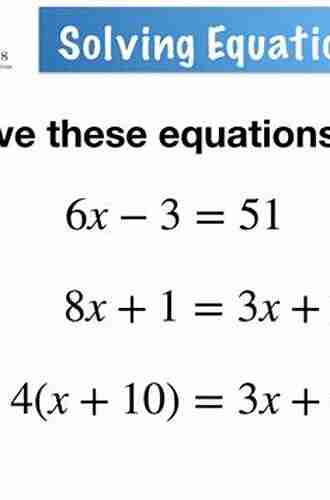
















Do you want to contribute by writing guest posts on this blog?
Please contact us and send us a resume of previous articles that you have written.
Functional Equations And How To Solve Them Problem In Mathematics

Welcome to a fascinating journey into the world of functional equations in mathematics! In this article, we will explore the concept of functional equations, understand their significance, and learn effective strategies to solve them. So, let's dive right into it!
What are Functional Equations?
In mathematics, functional equations are equations involving unknown functions. These equations typically define a relationship between the values of a function and its arguments or inputs. Functional equations play a vital role in various fields of mathematics, including analysis, number theory, algebra, and more.
A functional equation is typically represented in the form:
4.2 out of 5
| Language | : | English |
| File size | : | 3410 KB |
| Screen Reader | : | Supported |
| X-Ray for textbooks | : | Enabled |
| Print length | : | 143 pages |
F(x) = y
where 'F' denotes the unknown function, 'x' represents the variables or inputs, and 'y' represents the outputs or values of the function.
Importance of Solving Functional Equations
Functional equations are not merely abstract mathematical constructs. They have applications in a wide range of areas, including physics, economics, computer science, and engineering. Solving functional equations allows us to model and describe real-world phenomena, make predictions, and solve intricate problems.
Types of Functional Equations
Functional equations can be classified into different types based on their properties and characteristics. Let's explore some common types:
- Linear Functional Equations: These equations involve linear functions and typically have a straightforward solution.
- Quadratic Functional Equations: These equations involve quadratic functions and often require more advanced techniques to solve.
- Homogeneous Functional Equations: These equations involve functions that satisfy additional properties, such as symmetry or constant multiples.
- Cauchy's Functional Equation: This fundamental functional equation is named after Augustin-Louis Cauchy and has significant applications in mathematics.
Solving Functional Equations
Solving functional equations may seem challenging at first, but with the right approach and techniques, it becomes an exciting mathematical adventure. Here are some strategies to help you tackle functional equations:
- Substitution: Substitute known values or simplify the equation by replacing certain functions or variables.
- Restriction: Apply constraints on the variables to narrow down the potential solutions.
- Recursive Relations: Utilize recursive relations by expressing the unknown function in terms of previous values or inputs.
- Functional Analysis: Employ techniques from functional analysis, such as fixed points, continuity, and differentiability.
- Induction: Use mathematical induction to prove properties or identify patterns in the functional equation.
- Approximation: Employ approximation methods to estimate the behavior of the function.
Examples and Applications
Let's explore a couple of examples to see how functional equations arise in real-world problems:
- Example 1: Fibonacci Sequence: The Fibonacci sequence is a classic example of a recursive functional equation. It defines a sequence of numbers where each number is the sum of the two preceding ones. The functional equation can be expressed as:
F(n) = F(n-1) + F(n-2)
- Example 2: Logistic Growth Model: In biology and population dynamics, the logistic growth model is often used to describe the growth of a population over time. The equation incorporates a limiting factor that constrains the exponential growth. The functional equation can be represented as:
F(t) = k * F(t-1) * (1 - F(t-1)/L)
These examples highlight how functional equations arise in various disciplines and provide valuable insights into the behavior of complex systems.
Functional equations are powerful tools for modeling and solving intricate mathematical problems. By understanding their concepts, properties, and techniques for solving them, you can explore the depths of mathematics and unlock new avenues of knowledge. So, embrace the challenge, sharpen your problem-solving skills, and embark on a fascinating journey through functional equations!
4.2 out of 5
| Language | : | English |
| File size | : | 3410 KB |
| Screen Reader | : | Supported |
| X-Ray for textbooks | : | Enabled |
| Print length | : | 143 pages |
Many books have been written on the theory of functional equations, but very few help readers solve functional equations in mathematics competitions and mathematical problem solving. This book fills that gap. Each chapter includes a list of problems associated with the covered material. These vary in difficulty, with the easiest being accessible to any high school student who has read the chapter carefully. The most difficult will challenge students studying for the International Mathematical Olympiad or the Putnam Competition. An appendix provides a springboard for further investigation of the concepts of limits, infinite series and continuity.

 Samuel Ward
Samuel WardTake Control Of Your Network Marketing Career
Are you tired of working...

 Bryson Hayes
Bryson HayesThe Enigmatic Talent of Rype Jen Selk: A Musical Journey...
When it comes to musical prodigies,...

 Norman Butler
Norman ButlerUnveiling the Rich History and Poetry of Shiraz in...
When it comes to the cultural...

 Cade Simmons
Cade SimmonsHow Impatience Can Be Painful In French And English
: In today's fast-paced world, impatience...

 William Shakespeare
William ShakespeareSewing For Sissy Maids - Unleashing Your Creative Side
Are you ready to dive...

 Harry Hayes
Harry HayesGST Compensation to States: Ensuring Fiscal Stability...
In the wake of the COVID-19 pandemic,...

 Rodney Parker
Rodney ParkerLearn How to Play Blackjack: A Comprehensive Guide for...
Blackjack, also known as twenty-one, is one...

 Wade Cox
Wade CoxComplete Guide Through Belgium And Holland Or Kingdoms Of...
Welcome, travel enthusiasts, to a...

 Jack Butler
Jack Butler15 Eye Popping Projects To Create with Felt Decorations
Felt decorations have become a popular craft...

 Dennis Hayes
Dennis HayesFirst Aid For Teenager Soul Mini Book Charming Petites...
The teenage years can...

 Brett Simmons
Brett SimmonsFrom Fear To Freedom - Overcoming Your Fears and Living a...
Are you tired of living in...

 Carl Walker
Carl WalkerSmoking Ears And Screaming Teeth: The Shocking Truth...
Smoking has long been known to cause a host of...
Light bulbAdvertise smarter! Our strategic ad space ensures maximum exposure. Reserve your spot today!

 Jesus MitchellThe Game of Lacrosse: Boys and Girls Versions | How to Play Lacrosse | Player...
Jesus MitchellThe Game of Lacrosse: Boys and Girls Versions | How to Play Lacrosse | Player...
 Henry David ThoreauGun Violence Prevention And Community Safety Act Of 2020 5717: Keeping Our...
Henry David ThoreauGun Violence Prevention And Community Safety Act Of 2020 5717: Keeping Our... Edward ReedFollow ·2.2k
Edward ReedFollow ·2.2k Mark TwainFollow ·5.7k
Mark TwainFollow ·5.7k Gordon CoxFollow ·14.8k
Gordon CoxFollow ·14.8k Kevin TurnerFollow ·9k
Kevin TurnerFollow ·9k Devin RossFollow ·10.6k
Devin RossFollow ·10.6k Junot DíazFollow ·2.1k
Junot DíazFollow ·2.1k Steven HayesFollow ·12.8k
Steven HayesFollow ·12.8k Patrick HayesFollow ·8.7k
Patrick HayesFollow ·8.7k